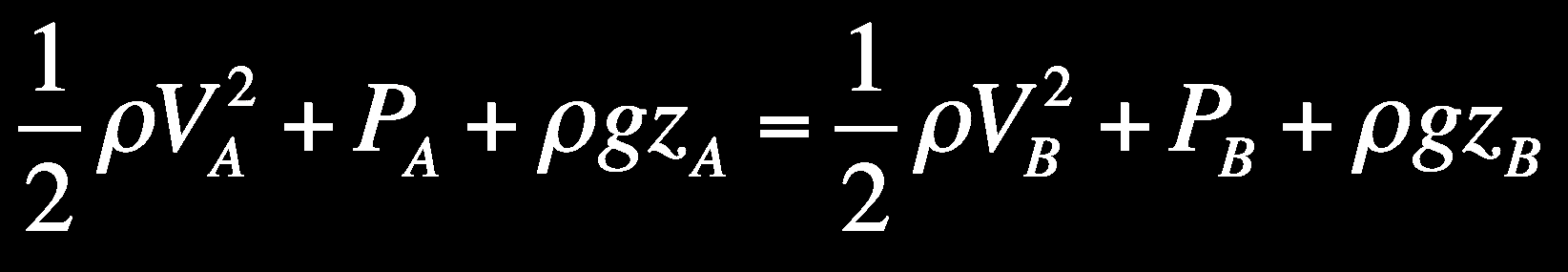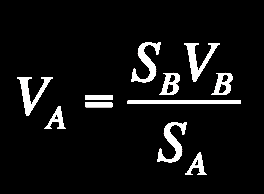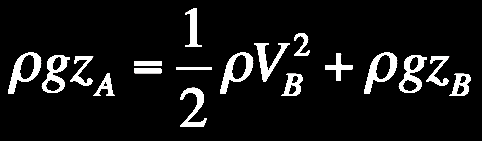Notre clepsydre
Notre clepsydre :
Nous avons fabriqué notre clepsydre avec deux bouteilles d’eau.
Nous avons tout d’abord collé deux bouchons entre eux avec un pistolet à colle. Une fois bien collé, nous les avons percés avec une perceuse munie d’un très petit foret. Nous avons fait un petit trou sur celle du bas et coupé le haut de la bouteille du haut pour que la pression soit la même et que l’eau coule normalement. La clepsydre est fabriquée !
Voici la vidéo qui montre cette fabrication et la clepsydre en fonctionnement: Fabrication d'une Clepsydre
Nous avons ensuite effectué quelques calculs. Nous avons fait une marque sur la bouteille du bas tous les 100 ml, puis rempli la clepsydre au maximum et noté le temps à chaque graduation passée et la hauteur du liquide dans la bouteille du haut. Grâce à ces mesures, il a été possible de calculer le débit à chaque 100 ml et d’obtenir une courbe du débit en fonction du temps ce qui prouve que le débit n’est pas constant.
En 1738, Bernoulli, mathématicien suisse propose une formule très importante pour la mécanique des fluides.
Détaillons un peu le théorème de Bernoulli pour obtenir la vitesse d'écoulement de la clepsydre.
L'écoulement du fluide doit tout d'abord vérifier certaines hypothèses :
- il doit être stationnaire (c'est à dire qu'il ne dépend pas du temps)
- il doit être non visqueux
- il doit être incompressible
- les forces extérieures qui s'excercent sur le fluide sont seulement liées à la gravitation
Sous ses hypothèses, la formule de Bernoulli est :
ρ : Masse volumique du fluide
P : Pression du fluide
z : Ordonné du point considéré
V : Vitesse du fluide du point considéré
g : Accélération de la pesanteur
Le théorème traduit une conservation de l'énergie au sein du fluide. Le premier terme correspond à l'énergie cinétique du fluide, le second correspond à l'énergie liée à la pression et le troisième à la gravité.
Dans une clepsydre à débit constant, le débit au point A est le même que le débit au point B : SA x VA = SB x VB
Dans la clepsydre, SA>>SB
On en déduit que : VA<<VB
Ce qui équivaut à : VA2<<VB2
Dans l’expression :
Nous pouvons donc enlever le terme : 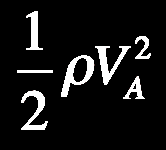
La pression est la même aux deux points A et B et elle est égale à la pression atmosphérique.
Et la vitesse du jet d’eau est : ![]()
Si on se place dans le repère où ZB= 0 et ZA = Z, la vitesse d’écoulement de la clepsydre est de : 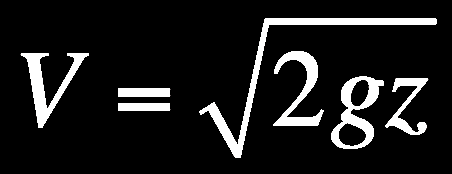
Ajouter un commentaire